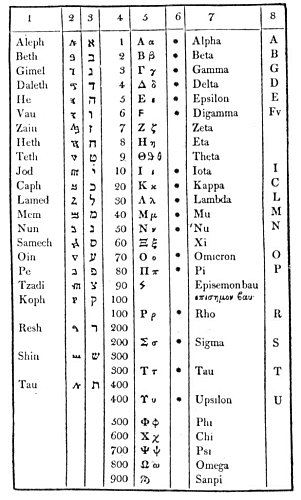
p. 81
HARMONY is a state recognized by great philosophers as the immediate prerequisite of beauty. A compound is termed beautiful only when its parts are in harmonious combination. The world is called beautiful and its Creator is designated the Good because good perforce must act in conformity with its own nature; and good acting according to its own nature is harmony, because the good which it accomplishes is harmonious with the good which it is. Beauty, therefore, is harmony manifesting its own intrinsic nature in the world of form.
The universe is made up of successive gradations of good, these gradations ascending from matter (which is the least degree of good) to spirit (which is the greatest degree of good). In man, his superior nature is the summum bonum. It therefore follows that his highest nature most readily cognizes good because the good external to him in the world is in harmonic ratio with the good present in his soul. What man terms evil is therefore, in common with matter, merely the least degree of its own opposite. The least degree of good presupposes likewise the least degree of harmony and beauty. Thus deformity (evil) is really the least harmonious combination of elements naturally harmonic as individual units. Deformity is unnatural, for, the sum of all things being the Good, it is natural that all things should partake of the Good and be arranged in combinations that are harmonious. Harmony is the manifesting expression of the Will of the eternal Good.
THE PHILOSOPHY OF MUSIC
It is highly probable that the Greek initiates gained their knowledge of the philosophic and therapeutic aspects of music from the Egyptians, who, in turn, considered Hermes the founder of the art. According to one legend, this god constructed the first lyre by stretching strings across the concavity of a turtle shell. Both Isis and Osiris were patrons of music and poetry. Plato, in describing the antiquity of these arts among the Egyptians, declared that songs and poetry had existed in Egypt for at least ten thousand years, and that these were of such an exalted and inspiring nature that only gods or godlike men could have composed them. In the Mysteries the lyre was regarded as the secret symbol of the human constitution, the body of the instrument representing the physical form, the strings the nerves, and the musician the spirit. Playing upon the nerves, the spirit thus created the harmonies of normal functioning, which, however, became discords if the nature of man were defiled.
While the early Chinese, Hindus, Persians, Egyptians, Israelites, and Greeks employed both vocal and instrumental music in their religious ceremonials, also to complement their poetry and drama, it remained for Pythagoras to raise the art to its true dignity by demonstrating its mathematical foundation. Although it is said that he himself was not a musician, Pythagoras is now generally credited with the discovery of the diatonic scale. Having first learned the divine theory of music from the priests of the various Mysteries into which he had been accepted, Pythagoras pondered for several years upon the laws governing consonance and dissonance. How he actually solved the problem is unknown, but the following explanation has been invented.
One day while meditating upon the problem of harmony, Pythagoras chanced to pass a brazier’s shop where workmen were pounding out a piece of metal upon an anvil. By noting the variances in pitch between the sounds made by large hammers and those made by smaller implements, and carefully estimating the harmonies and discords resulting from combinations of these sounds, he gained his first clue to the musical intervals of the diatonic scale. He entered the shop, and after carefully examining the tools and making mental note of their weights, returned to his own house and constructed an arm of wood so that it: extended out from the wall of his room. At regular intervals along this arm he attached four cords, all of like composition, size, and weight. To the first of these he attached a twelve-pound weight, to the second a nine-pound weight, to the third an eight-pound weight, and to the fourth a six-pound weight. These different weights corresponded to the sizes of the braziers’ hammers.

Moe is the founder of GnosticWarrior.com. He is a father, husband, author, martial arts black belt, and an expert in Gnosticism, the occult, and esotericism.